Апостериорная плотность вероятности при синтезе систем слежения за амплитудой сигнала и СКО шума

Версия 22:59, 16 апреля 2011

Начал проводить синтез СС, остановился перед задачей нахождения экстремума.

Постановка задачи

Полагаем, что на входе системы обработки на интервале времени $\!\!T=L{{T}_{d}}\!\!$ наблюдается реализация

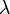${{y}_{k,l}}=S\left( {{t}_{k,l}},\text{ }\!\!\lambda\!\!\text{ },\text{ }\!\!\mu\!\!\text{ } \right)+\sigma _{n,k}^{{}}{{n}_{k,l}},$ $l=\overline{1,L},$

где $\text{ }\!\!\lambda\!\!\text{ }$ , $\text{ }\!\!\mu\!\!\text{ }$ ― постоянные на интервале наблюдения информативные и неинформативные параметры сигнала; $\!\!n_{k,l}\!\!$ — ДБГШ с нулевым математическим ожиданием и единичной дисперсией.

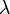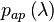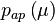При статистическом подходе к решению задач оценивания параметры $\text{ }\!\!\lambda\!\!\text{ }$ , $\text{ }\!\!\mu\!\!\text{ }$ полагаются векторными СВ с заданными априорными плотностями вероятности ${{p}_{ap}}\left( \text{ }\!\!\lambda\!\!\text{ } \right)$ , ${{p}_{ap}}\left( \text{ }\!\!\mu\!\!\text{ } \right)$ .

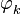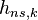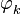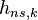Пусть решается задача оценки одного или нескольких параметров сигнала, полагая при этом, что начальная фаза сигнала $\varphi _{k}^{{}}$ и символ навигационного сообщения $\!\!h_{ns,k}\!\!$ являются СВ, причем $\varphi _{k}^{{}}$ распределена равномерно на интервале $\left[ -\pi ,\pi \right]$ , а ${\!\!{h}_{ns,k}\!\!}$ принимает значения 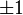$\pm 1$ с равными вероятностями.

Модель сигнала может быть записана в виде

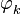$S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}^{{}}{{h}_{ns,k}}{{G}_{dc}}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\varphi _{k}^{{}} \right),$

где $\varphi _{k}^{{}}$ распределена равномерно на интервале $\left[ -\pi ,\pi \right]$ .

Рассмотрим некогерентный режим НАП, при котором не используется и не формируется информация о фазе сигнала 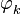$\varphi _{k}^{{}}$ и символе НС 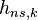$\!\!{h}_{ns,k}\!\!$ , т.е. данные параметры полагаются неинформативным 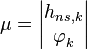$\mathbf{\mu }=\left| \begin{matrix} {{h}_{ns,k}} \\ \varphi _{k}^{{}} \\ \end{matrix} \right|$ . 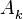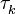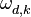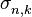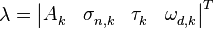Тогда вектор информативных параметров состоит из $A_{k}^{{}}$ , $\tau _{k}^{{}}$ , $\omega _{d,k}^{{}}$ и $\sigma _{n,k}^{{}}$ : $\mathbf{\lambda }=\left| \begin{matrix} A_{k}^{{}} & \sigma _{n,k}^{{}} & \tau _{k}^{{}} & \omega _{d,k}^{{}} \\ \end{matrix} \right|_{{}}^{T}$ .

Выражение для апостериорной плотности вероятности

После ряда преобразований получаем выражение для апостериорной плотности вероятности:

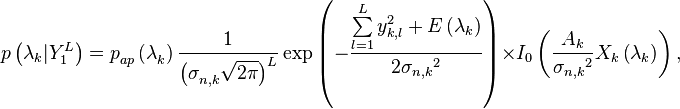
$p\left( {{\mathbf{\lambda }}_{k}}|Y_{1}^{L} \right)=p_{ap}^{{}}\left( \mathbf{\lambda }_{k}^{{}} \right)\frac{1}{\left( \sigma _{n,k}^{{}}\sqrt{2\pi } \right)_{{}}^{L}}\exp \left( -\frac{\sum\limits_{l=1}^{L}{y_{k,l}^{2}}+E\left( {{\mathbf{\lambda }}_{k}} \right)}{2{{\sigma }_{n,k}}^{2}} \right)\times {{I}_{0}}\left( \frac{{{A}_{k}}}{{{\sigma }_{n,k}}^{2}}{{X}_{k}}\left( {{\mathbf{\lambda }}_{k}} \right) \right),$

где

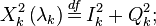
$X_{k}^{2}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,I_{k}^{2}+Q_{k}^{2};$

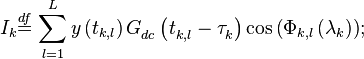
${{I}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\cos \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)};$

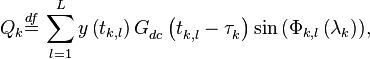
${{Q}_{k}}\overset{df}{\mathop{=}}\,\sum\limits_{l=1}^{L}{y\left( {{t}_{k,l}} \right)G_{dc}^{{}}\left( t_{k,l}^{{}}-\tau _{k}^{{}} \right)\sin \left( {{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right) \right)},$

в которых

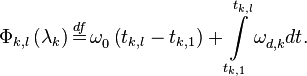
${{\Phi }_{k,l}}\left( {{\mathbf{\lambda }}_{k}} \right)\overset{df}{\mathop{=}}\,\omega _{0}^{{}}\left( {{t}_{k,l}}-{{t}_{k,1}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}.$

Дальнейшие действия

Далее надо решить задачу нахождения экстремума, что при получившемся выражении - не самое приятное занятие. Вероятно, более легкий и позитивный путь - синтез исходя из статистических эквивалентов корреляторов.

— Корогодин Илья • 00:47, 11 апреля 2011 • нет комментариев

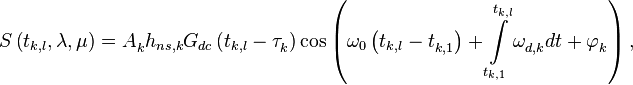
[ Хронологический вид ]Комментарии

(нет элементов)

Войдите, чтобы комментировать.

@@ Строка 5: / Строка 5: @@
 Полагаем, что на входе системы обработки на интервале времени <math>\!\!T=L{{T}_{d}}\!\!</math> наблюдается реализация
-<math>{{y}_{k,l}}=S\left( {{t}_{k,l}},\text{ }\!\!\lambda\!\!\text{ },\text{ }\!\!\mu\!\!\text{ } \right)+\sigma _{n,k}^{{}}{{n}_{k,l}},</math> &nbsp; <math>l=\overline{1,L},</math>
+:<math>{{y}_{k,l}}=S\left( {{t}_{k,l}},\text{ }\!\!\lambda\!\!\text{ },\text{ }\!\!\mu\!\!\text{ } \right)+\sigma _{n,k}^{{}}{{n}_{k,l}},</math> &nbsp; <math>l=\overline{1,L},</math>
 где <math>\text{ }\!\!\lambda\!\!\text{ }</math>, <math>\text{ }\!\!\mu\!\!\text{ }</math> ― постоянные на интервале наблюдения информативные и неинформативные параметры сигнала; <math>\!\!n_{k,l}\!\!</math> — ДБГШ с нулевым математическим ожиданием и единичной дисперсией.
@@ Строка 19: / Строка 19: @@
 Модель сигнала может быть записана в виде
-<math>S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}^{{}}{{h}_{ns,k}}{{G}_{dc}}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\varphi _{k}^{{}} \right),</math>
+:<math>S\left( {{t}_{k,l}},\mathbf{\lambda },\mathbf{\mu } \right)=A_{k}^{{}}{{h}_{ns,k}}{{G}_{dc}}\left( {{t}_{k,l}}-\tau _{k}^{{}} \right)\cos \left( {{\omega }_{0}}\left( {{t}_{k,l}}-t_{k,1}^{{}} \right)+\int\limits_{{{t}_{k,1}}}^{{{t}_{k,l}}}{\omega _{d,k}^{{}}dt}+\varphi _{k}^{{}} \right),</math>
 где <math>\varphi _{k}^{{}}</math> распределена равномерно на интервале <math>\left[ -\pi ,\pi  \right]</math>.
@@ Строка 30: / Строка 30: @@
     A_{k}^{{}} & \sigma _{n,k}^{{}} & \tau _{k}^{{}} & \omega _{d,k}^{{}}  \\
 \end{matrix} \right|_{{}}^{T}</math>.
 == Выражение для апостериорной плотности вероятности ==

Апостериорная плотность вероятности при синтезе систем слежения за амплитудой сигнала и СКО шума

Версия 22:59, 16 апреля 2011

Постановка задачи

Выражение для апостериорной плотности вероятности

Дальнейшие действия

[ Хронологический вид ]Комментарии

Персональные инструменты

Пространства имён

Варианты

Просмотры

Действия

Поиск

SRNS Wiki

Рабочие журналы

Приватный файлсервер

QNAP Сервер

Инструменты